轉(zhuǎn)爐用扭力桿系統(tǒng)振動理論研究
吳林峰，王文
( 華北水利水電大學機械學院，鄭州450008)
摘要: 扭力桿系統(tǒng)的動態(tài)特性對轉(zhuǎn)爐設(shè)備工作的可靠性有著重要影響，研究其振動頻率和陣型是設(shè)備自主創(chuàng)新的關(guān)鍵技術(shù)之一。綜合考慮扭力桿系統(tǒng)實際結(jié)構(gòu)組成，提出了均質(zhì)桿和集中質(zhì)量桿一端鉸支另一端簡支反對稱彎曲振動梁、均質(zhì)桿和集中質(zhì)量桿一端固支另一端簡支反對稱彎曲振動梁等四種振動模型。以某廠150t氧氣頂吹轉(zhuǎn)爐扭力桿系統(tǒng)為例進行了理論計算。結(jié)果表明，扭力桿系統(tǒng)振動模型采用集中質(zhì)量桿一端固支和一端簡支反對稱彎曲振動梁模型更合理。并用有限元法對其正確性進行了驗證，兩種方法的計算結(jié)果吻合，都可以對扭力桿系統(tǒng)進行研究，但是理論解更為簡單方便，便于工程技術(shù)人員直接引用，為指導工程實際設(shè)計和生產(chǎn)提供了理論基礎(chǔ)。
關(guān)鍵詞: 轉(zhuǎn)爐；扭力桿系統(tǒng)； 振動梁模型；理論解；有限元解
扭力桿能夠利用自身的彈性扭轉(zhuǎn)變形儲備能量、傳遞扭矩、協(xié)調(diào)輸出力矩平衡及在柔性支撐中取代體積較大的軸承等功能，在大小型設(shè)備上都得到了廣泛的應(yīng)用［1］。對于扭力桿( 系統(tǒng)) 的研究，有數(shù)值法［2 － 3］、實驗測試法［4］、剛度精度求解法［5 － 6］以及利用攝動法進行可靠性設(shè)計［7］等方法。以上研究都是對扭力桿系統(tǒng)進行的靜態(tài)研究。
大型轉(zhuǎn)爐用扭力桿用于儲存現(xiàn)代轉(zhuǎn)爐快速搖爐傾動過程的沖擊振動，是減緩快速搖爐對傳動系統(tǒng)的沖擊，避免潑鋼等惡性事故發(fā)生，保障生產(chǎn)安全的重要組成部分。扭力桿系統(tǒng)的靜態(tài)研究不能完全滿足生產(chǎn)需要，而對扭力桿( 系統(tǒng)) 的動態(tài)特性研究只有鄭龍捷［8］對大噸位用扭力桿異常振動進行了研究。
我國對于大型轉(zhuǎn)爐設(shè)備建設(shè)，目前依靠引進國外設(shè)計技術(shù)，利用國內(nèi)制作和安裝技術(shù)進行建造［9］。同時設(shè)備引進時，加之國外對相關(guān)技術(shù)的保密，沒有任何產(chǎn)品相關(guān)的核心技術(shù)，國內(nèi)對大型轉(zhuǎn)爐的設(shè)計技術(shù)和使用技術(shù)一直處于探索階段，嚴重束縛了轉(zhuǎn)爐煉鋼設(shè)備的自主創(chuàng)新與開發(fā)。因此，對扭力桿系統(tǒng)進行動態(tài)理論研究，具有重要的理論指導和工程應(yīng)用價值。
本文綜合考慮轉(zhuǎn)爐用扭力桿系統(tǒng)可能存在的振動模型，提出新的扭振理論設(shè)計方法，并進行三維全尺寸有限元數(shù)值計算，對理論方法的可行性進行驗證。
1 扭力桿系統(tǒng)振動模型建立
扭力桿位于減速機箱體下方，安裝在兩端支承軸承座上。爐體制動時，由于爐體與減速機整體繞耳軸轉(zhuǎn)動，減速機下部左右兩傳力曲柄，一個受拉，一個受壓，將傾動機構(gòu)傳來的力矩傳遞給扭力桿，在曲柄兩端形成大小相等、方向相反的一對力偶，使扭力桿發(fā)生扭轉(zhuǎn)變形從而起到支撐與緩沖作用［10］。對于呈現(xiàn)空間布置的扭力桿而言，其振動模態(tài)復雜，包括扭轉(zhuǎn)模態(tài)，縱向彎曲模態(tài)，橫向彎曲模態(tài)等。實際工作中，與扭力桿系統(tǒng)工作特性最相關(guān)的是傾動自振模態(tài)，就是扭力桿曲柄對扭力桿軸線的反對稱的彎曲模態(tài)。因此，研究扭力桿對自振模態(tài)的傾動自振頻率成為研究的關(guān)鍵。
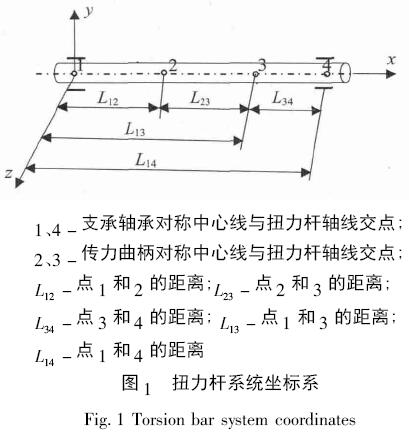
對扭力桿系統(tǒng)建立如圖1所示的坐標系，規(guī)定扭力桿軸為x軸，其中有軸向竄動的一端為正向，有軸向定位一端的支承軸承對稱中心線與x軸的交點為原點(記為點1) ，兩個傳力曲柄對稱中心線與扭力桿軸線交點記為2和3，有軸向竄動的支承軸承對稱中心線與扭力桿軸線的交點記為點4。
1． 1 均質(zhì)桿一端鉸支、一端簡支反對稱彎曲振動模型———模型一
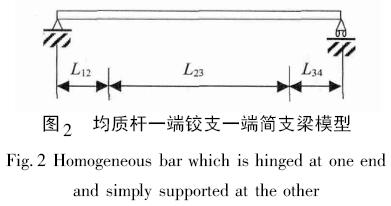
如果僅考慮扭力桿質(zhì)量，不考慮傳力曲柄、傳力塊和卡盤質(zhì)量，將扭力桿等效為一等直圓桿(如圖2所示)，有軸向定位的一端簡化為鉸支端、允許有軸向竄動的一端簡化為簡支端，則該振動模態(tài)對應(yīng)簡支梁振動的二階模態(tài)。根據(jù)振動理論的研究結(jié)果［11 － 13］，該均質(zhì)桿一端鉸支、一端簡支反對稱彎曲振動模型模態(tài)圓頻率為
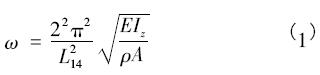
式中，E為彈性模量，Iz為扭力桿對z軸的轉(zhuǎn)動慣量，ρ為材料密度，A為扭力桿截面積。歸一化后的模態(tài)振幅為
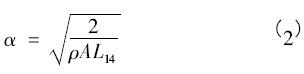
1． 2 集中質(zhì)量桿一端鉸支、一端簡支反對稱彎曲振動模型———模型二
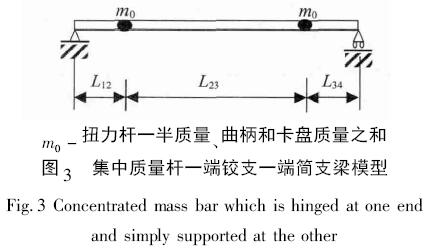
如果考慮傳力曲柄、傳力塊和卡盤質(zhì)量，將扭力桿的質(zhì)量分兩部分考慮，分別和卡盤、曲柄質(zhì)量看作兩個集中質(zhì)量塊(作用在曲柄對稱中心線與扭力桿軸線交點2和點3處) 。建立一端鉸支一端簡支梁模型(如圖3所示) ，利用集中質(zhì)量法和瑞利法進行求解。
設(shè)模態(tài)函數(shù)為
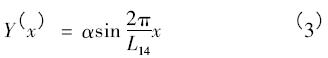
則根據(jù)振動動能等于振動變形的關(guān)系得到振動圓頻率為
1． 3 均質(zhì)桿一端固支、一端簡支反對稱彎曲振動模型———模型三
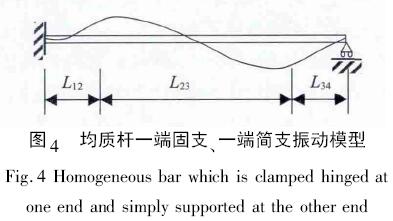
由于軸承有一定的寬度，其實際對扭力桿的支承，還不完全等同于鉸支。為此，將扭力桿有軸向定位的一端簡化為固支端，允許軸向竄動的一端簡化為簡支端(不考慮傳力曲柄、傳力塊和卡盤質(zhì)量) ，模型如圖4所示。
根據(jù)模型計算得到的二階模態(tài)的圓頻率公式為
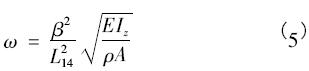
式中，β = 2． 25π。
振幅為
1． 4 集中質(zhì)量桿一端固支、一端簡支反對稱彎曲振動模型———模型四
考慮傳力曲柄、傳力塊和卡盤質(zhì)量，利用集中質(zhì)量法，所建立的模型如圖5所示(有軸向定位的一端簡化為固支端、允許有軸向竄動的一端簡化為簡支端) 。
選取模態(tài)函數(shù)為
則根據(jù)振動動能等于振動變形的關(guān)系得到圓頻率為
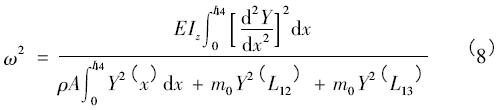
2 質(zhì)量對振動頻率的影響
由式(1) 、式(2) 、式(4) 、式(5) 、式(6) 和式(8) 可推知不同模型扭力桿系統(tǒng)的圓頻率和振幅大小，再由頻率和圓頻率的關(guān)系求出頻率的大小。以某廠設(shè)計的150t氧氣頂吹轉(zhuǎn)爐扭力桿系統(tǒng)設(shè)計參數(shù)為例(如表1所示) 進行計算，得到扭力桿系統(tǒng)的圓頻率和固有頻率以及振幅大小(如表2所示) 。
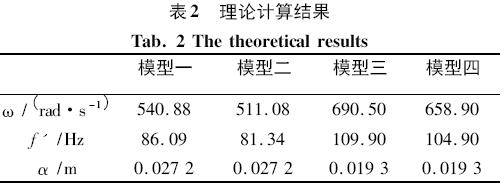
從表2計算結(jié)果可知：模型一和模型二兩者的圓頻率相差29．80 rad /s，頻率相差4．75 Hz，兩者振幅相等，這說明曲柄、傳力塊和卡盤質(zhì)量對一端固鉸支、一端簡支梁模型振動影響差別不是很大； 模型三和模型四兩者的圓頻率相差31．60 rad/s，頻率相差5．00Hz，這說明曲柄、傳力塊和卡盤質(zhì)量對一端固支、一端簡支反對稱彎曲振動模型影響差別也不是很大。但是，質(zhì)量對梁不同支承端方式影響很大，比如模型一二和模型三、四相比，圓頻率、頻率和振幅分別最大相差179．41 rad/s、28．56Hz 和7．9mm，這說明質(zhì)量對扭力桿系統(tǒng)頻率和振幅的影響不能忽略，結(jié)合扭力桿系統(tǒng)結(jié)構(gòu)的實際情況：扭力桿系統(tǒng)，以扭力桿為主體，主體上有用來傳遞扭矩的曲柄、卡盤和傳力塊、在兩端有支承軸承(一端用來軸向定位，一端有軸向竄動)，這些結(jié)構(gòu)相對于扭力桿系統(tǒng)來說，質(zhì)量影響不容忽視，模型分析中不能忽略。因此扭力桿模型研究考慮真實情況結(jié)果是: 即選擇集中質(zhì)量桿模型，同時扭力桿本體實際上是一端軸向固定、另一端是可以軸向竄動的模型比較接近實際，因此，選擇模型四分析扭力桿系統(tǒng)更為準確和合理。
3 有限元計算結(jié)果分析
圖2～圖5所示的模型理論計算時作了一定簡化，例如，扭力桿本體軸向尺寸是變截面的、曲柄和卡盤長度非定尺寸，而理論分析計算是看作固定尺寸分析的，軸承有一定的寬度而理論分析中沒有考慮，這些與扭力桿系統(tǒng)結(jié)構(gòu)的真實尺寸還存在一定的差別，有必要用較為真實的三維結(jié)構(gòu)模型和接觸傳力方式進行有限元計算，分析相應(yīng)的簡化對計算結(jié)果造成的影響。為了驗證理論公式的合理性，考慮實際工況的接觸傳力方式，對扭力桿系統(tǒng)進行了三維全尺寸結(jié)構(gòu)模型有限元方法數(shù)值計算。數(shù)值模擬扭力桿振動特性，通過對比分析，驗證理論設(shè)計方法的可靠性和精度。
在模型中，充分考慮扭力桿兩端軸頸與軸承座的軸瓦接觸、傳力曲柄梅花軸頭與扭力桿端部的接觸，選用柔體－柔體的面－面接觸形式，選用非線性算法［14］進行接觸計算。
表3為有限元方法計算得到的扭力桿五階自振頻率，圖6為扭力桿系統(tǒng)第一階振動模態(tài)。結(jié)果顯示，一階模態(tài)是豎向反對稱彎曲模態(tài)，二階模態(tài)為水平反對稱彎曲模態(tài)，三階模態(tài)為水平對稱彎曲模態(tài)，四階模態(tài)為豎向?qū)ΨQ彎曲模態(tài)，五階模態(tài)為扭轉(zhuǎn)模態(tài)。
考慮傳力曲柄、傳力塊和卡盤質(zhì)量的集中質(zhì)量的一端固支、一端簡支的梁模型理論計算(模型四) 的一階頻率104．9Hz，與有限元方法計算的一階頻率107．70Hz值相差僅2．6%。模型四計算得到的模態(tài)振幅為0．019 25m，有限元計算一階振幅為0．027m，兩者相差28．7%。理論解比有限元解小，其原因是理論計算值只考慮了曲柄、傳力塊、卡盤的質(zhì)量，沒有考慮其相應(yīng)的幾何尺寸，有限元解將兩者都考慮了，所以理論解的模態(tài)幅值是指扭力桿上的值，而有限元解的模態(tài)幅值是指曲柄端部的幅值。以上誤差屬于工程設(shè)計使用的誤差范圍之內(nèi)，理論模型四相應(yīng)的頻率、振幅計算公式可以用來支持實際工程設(shè)計應(yīng)用，尤其是振動頻率的理論公式，對研究扭力桿系統(tǒng)振動特性的通用性研究具有重要的指導意義。
該部分設(shè)計，結(jié)合轉(zhuǎn)爐其他結(jié)構(gòu)部分的設(shè)計，開發(fā)的150t國產(chǎn)化新轉(zhuǎn)爐，轉(zhuǎn)爐自2007年正式投入生產(chǎn)以來，搖爐速度為1．60r/mim，整個設(shè)備工作正常。該扭力桿系統(tǒng)的固有頻率遠遠高于轉(zhuǎn)爐設(shè)備的工作頻率，避開了發(fā)生共振的可能，可用以指導煉鋼生產(chǎn)實際。
4 結(jié)論
本文綜合考慮了扭力桿系統(tǒng)可能存在的四種模型并推導出四種模型的圓頻率和振幅理論公式。并以150t 轉(zhuǎn)爐扭力桿系統(tǒng)對四種模型進行討論，得出扭力桿系統(tǒng)集中質(zhì)量桿一端固支、一端簡支梁模型更符合實際。又用有限元法對該模型理論解進行了對比，得出以下結(jié)論：
(1) 集中質(zhì)量桿一端固支、一端簡支梁模型(模型四) 更符合扭力桿系統(tǒng)振動研究。
(2) 模型四的振動頻率和振幅理論公式在同類扭力桿系統(tǒng)設(shè)計時，只需要將扭力桿系統(tǒng)的結(jié)構(gòu)尺寸代入，可以直接引用公式計算。
(3) 由于接觸非線性的引入，使有限元計算工作量增大，而理論公式的計算比有限元法簡單方便，更適合工程設(shè)計人員使用。
參 考 文 獻
［1］吳林峰，尹曉春．轉(zhuǎn)爐用變截面自平衡式扭力桿扭轉(zhuǎn)變形的理論計算［J］．工程力學，2012，29(6):47－51．
WU Linfeng，YIN Xiaochun． Calculation formala for torsionaldeformation of self-balanced torsion bar with variable crosssectionin convertor ［J］． Engineering mechanics，2012，29( 6) : 47 － 51．
［2］LEE K． A numerical method for dynamic analysis of trackedvehicles of high mobility［J］．Journal of Mechanical Scienceand Technology，2000，14 (10) : 1028 － 1040．
［3］余楊，高瞻．轉(zhuǎn)爐旋轉(zhuǎn)接頭扭力桿防旋轉(zhuǎn)裝置及有限元分析［J］． 鋼鐵技術(shù)，2010(1) : 8－12．
YU Yang，GAO Zhan．Finite element analysis of the antirotationdevice of rotary joint torsion bar in convertor ［J］．Iron ＆ Steel Technology，2010(1):8－12．
［4］BAＲTHELAT F，WU Z，PＲOＲOK B C，et al． Dynamictorsion testing of nanocrystalline coatings using high-speedphotography and digital image correlation［J］．ExperimentalMechanics，2003，43(3):331-340．
［5］ 劉春節(jié)，王正東． 圓形截面微型扭桿剛度的解析計算［J］． 工程力學，2009，26( 7) : 35 － 38．
LIU Chunjie，WANG Zhengdong． Analysis of torsion rigidityof micro bars with circular cross section［J］． Engineering
［6］趙燕．全懸掛轉(zhuǎn)爐扭力桿和耳軸的扭轉(zhuǎn)剛度分析［J］．北京聯(lián)合大學學報(自然科學版) ，2012，26(2):25－29．
ZHAO Yan．Torsion stiffness analysis of torque rod andtrunnion for full suspension convertor ［J］．Journal of Beijingunion University ( Natural Sciences ) ，2012，26 (2):25－29．
［7］張義民，賀向東，劉巧玲． 扭桿的可靠性優(yōu)化設(shè)計［J］．汽車技術(shù)，2002 ( 5) : 5 － 7．
ZHANG Yimin，HE Xiangdong，LIU Qiaoling． Ｒeliabilitydesign of torsion bar diameter ［J］．Automobile Technology，2002(5):5－7．
［8］鄭龍捷． 轉(zhuǎn)爐扭力桿工作過程異常振動原因分析與改進措施［J］． 冶金叢刊，2013( 5) : 37 － 41．
ZHENG Longjie．Analysis on abnormal vibration of torsion bardevice during operation and countermeasures ［J］．Metallurgical Collections，2013(5):37－41．
［9］齊堅，陶海銀． 國內(nèi)容量最大的全國產(chǎn)化下懸掛轉(zhuǎn)爐投產(chǎn)成功應(yīng)用多項中冶賽迪自主技術(shù)［J］．中國鋼鐵業(yè)，2009(5):31．
QI Jian，TAO Haiyin．The successful application ofindependent technology CISDI in Hanging converter with thedomestic production capacity of the largest one in the nationalproduction ［J］．China Steel，2009(5):31．
［10］吳林峰．轉(zhuǎn)爐托圈和扭力桿的設(shè)計理論分析［D］．南京:南京理工大學，2012．
［11］徐銘陶，周榮仁，趙邦義．振動分析基礎(chǔ)講義［M］．重慶:重慶大學力學教研室，1982．
［12］張阿舟，諸德超，姚啟航，等．振動理論與分析［M］．北京: 航空工業(yè)出版社，1996．
［13］吳福光，蔡成武，徐兆．振動理論［M］．北京: 高等教育出版社,1987．
［14］MOAVENI S．Finite element analysis—theory and applicationwith ANSYS［M］．3rd ed． Beijing: Electronic IndustryPress，2008.